|
The vortex possesses extremely high and diverse levels of energy that can be utilized for an abundance of practical applications in our society. Finding new, cleaner, cheaper, and innovative methods
of energy production and efficiency is a popular topic in today’s society and effects everyday engineering, economical, and political agendas. The energy potential of vortices has now been looked at closely as a possible answer for today’s energy dilemmas. One can see the immense energy
exhibited by the most familiar kind of vortex, a tornado. The shear forces caused by the rapid air velocity at the vortexial apex of the tornado are evidence of the vast amounts of energy a vortex can generate. The same principle is true for vortices in a body of water. The energy of the vortices can be used for several applications
by converting the mechanical energy of the vortices to other kinetic energy, such as electrical energy. This is the objective for the Hybrid Vortex Shedding (HYVOS)
experiments.
Vortex shedding is a phenomenon that occurs when the current flow of a body of water is disrupted by an obstruction, in this case a bluff body. When placed in a fluid flow most bodies create
a separated flow across a substantial proportion of their surface, thus classifying them as bluff. (Bearman). An unsteady flow is created due to the detachment of the stream of water that collides with the device. The turbulence these vortices create are pockets of energy that are usually viewed by
the engineering world as problems occurring naturally in air and water which can cause fatigue and failure to its man-made structures. Therefore, the behavior of vortices caused by the external flow of air or water past upright edifices has conventionally been studied by engineers and scientist defensively to find ways to eliminate
or guard against the affects of vortex shedding in their designs. In air, vortices create lift-induced drag on an aircraft and also cause vibrations against skyscrapers that can
possibly cause the failure of the structure in both instances. This behavior can be applied to vortices in water. These same vibrations occur as water flows past blunt obstructions in water, which causes flow separation and a boundary layer to form and very strong flow oscillations in the wake area behind the body. (Sihn). However
instead concentrating on the adverse affects of vortex shedding, one see that when harnessed, the energy generated by vortices can be used to convert mechanical
energy to electrical energy. Hybrid Vortex Shedding Renewable Energy System leads the way to a more innovative, sustainable, and economical alternative for energy production.
The original model for the HYVOS project was an oscillating water column. This energy conversion mechanism consisted of a cylindrical pipe with a small opening on the upstream side of the
body. The cylindrical pipe itself acts as an obstruction in the flux causing vortices to start forming on either side of the body. The opening allowed water to enter the cylindrical pipe where it can be observed that the pressure changes caused by the vortices and displayed in the pipe induced the
water column to act in a vertical oscillatory motion.
To test the validity of this device, other quantitative analysis had to be considered. These factors include the Reynolds number, flux, velocity under which experimentation takes places and
also the shape of the bluff body and other experimental variables. The vitality of these variables lies in the fact that it directly impacts the maximum potential amount of energy that can be extracted from the frequency of the oscillatory motion. The higher the Reynolds number, then the more turbulent
the water, therefore more kinetic energy can be obtained from the motion of the vortices. The Reynolds number is directly affected by the velocity of the water and diameter of the orifice and inversely proportional to the kinematic viscosity. A large Reynolds number indicates that the inertial forces are greater than the viscous
forces of the water. The Reynolds number is important because it can be used to understand whether or not it is a determining factor in the amount of energy that can be
extracted from vortices in the water. The Reynolds number under which testing takes place can be manipulated to figure out what optimal value would be needed to most efficiently create stronger and more frequently occurring vortices in the water in the prototype testing. This number can also be used to properly scale a real life model
to the prototype. The most favorable specifications and conditions for the real life model can be determined by equating the Reynolds number of the prototype
to that of the real life model. The same is true for other numbers such as the Strouhal’s number and Froude’s number. The Strouhal number is specifically importing in this testing because it relates the frequency of shedding to the velocity of the flow and a characteristic dimension of the body (diameter in the case
of a cylinder). It is defined as St = fstD / v where fst is the vortex shedding frequency (or the Strouhal frequency) of a body at rest, D is the diameter of the circular cylinder, and v is the
velocity of the ambient flow. These numbers can be found by the frequencies found from the oscillating water column and the velocity of the water. Both the Strouhal
number and the Froude number can serve as important factors for comparison and reference when building different prototypes and ultimately transferring the design to real world applications.
After several initial tests and analyses, the original design of the oscillating water column was revised, principally because of the effects of vortex shedding. Unfortunately, the oscillating water
column approach of the original design did not generate sufficient amounts of kinetic energy and therefore a more efficient method of energy conversion had to be envisioned. The new prototype is composed of a square or cylindrical bluff body with a fin positioned on the downstream side of the
body to serve as the oscillating component of the mechanism.
Vortex shedding is a regular occurrence of two-dimensional bluff body wakes and is present whether the separating boundary layers are laminar or turbulent. (Bearman). Vortex shedding and general
wake disturbances cause fluctuating pressures on the surface of the generating bluff body and if the body is flexible this can cause oscillations that are usually normal to the direction of flow, which was the case in the first prototype. There are different layers in the water column that cause
different types of vortex shedding. A professor describes the behavior of these water layers: “This shear layer will eventually roll into a discrete vortex and detach from the surface (a phenomenon called vortex shedding). Another type of flow instability emerges as the shear layer vortices shed from both the top and bottom
surfaces interact with one another.” (Shih). These types of instable energy have previously been unable to be harnessed to their fullest extent. “They shed alternatively from the
cylinder and generate a regular vortex pattern (the Karaman vortex street) in the wake (figure 2). The vortex shedding occurs at a discrete frequency and is a function of the Reynolds number.” (Shih). Thus, we can see that the Reynolds number as well as the Strouhal number has a large effect on the power of the vortices.
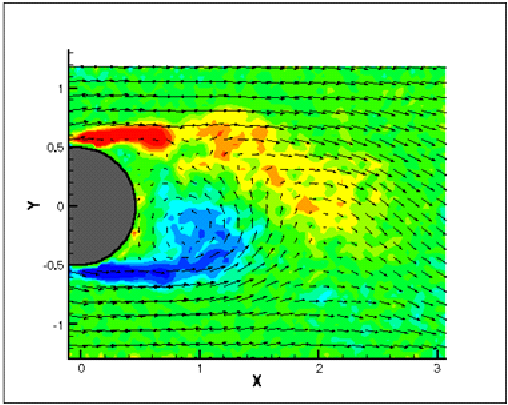 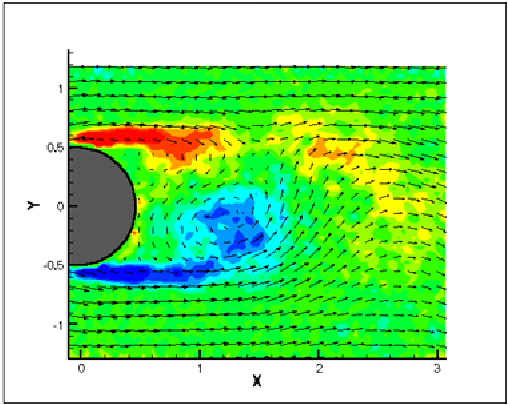
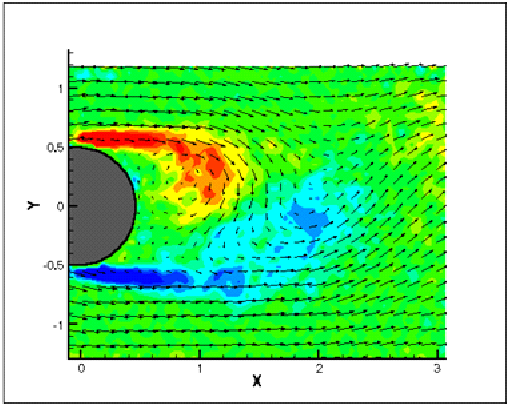 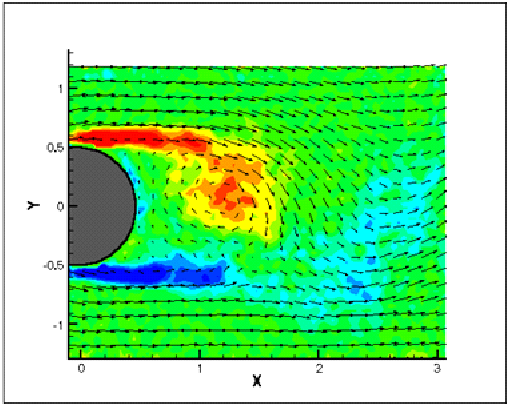
Figure 1. Four vector fields depicting different developing stages within a vortex shedding cycle are shown. Vortices are shed alternatively from the upper and lower surfaces of the cylinder, creating this periodic flow pattern. (Shih).
The vortex shedding frequency around a bluff body can be calculated as f
= Sr v / d where f = vortex shedding frequency (Hz), Sr = Strouhal number (dimensionless), v = flow velocity (m/s), and d = bluff body diameter. The figure below illustrates the concept of what occurs when water rushes against a bluff body and splits into two streamlines on either side of the bluff
body creating eddies of the downstream side of the bluff body. These
eddies are masses of water that are full of turbulent energy. These eddies or vortices are characterized by rotational motion while they also traverse the water. The two streamlines diverge into one set of vortices that rotate clockwise and another set of vortices that rotates counter-clockwise. The alternating manner of the rotary
motions of the vortices causes a system of high and low pressure. This change in pressure in the water can be physically seen by the
oscillatory motion of the fin. One set of vortices is trying to rotate in one direction while another set of vortices are opposing that motion by rotation in the other direction. This causes a back and forth movement by the fin. The vortices are in a sort of “boxing match” where one vortex is trying to push the other. The
stronger the “punches,” then the greater the amplitude of oscillations by the fin and thus more energy is can be extracted by the turbulent motion
of the water. (Dr. Fedele).
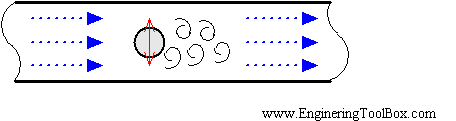 Figure 2. Vortex shedding
Source: www. Engineeringtoolbox.com
For the prototype to be tested, many different bluff body shapes and sizes will be considered as well as the size of the oscillating fin. Another variable of the prototype to be considered is whether or not to add
an attachment to the end of the oscillated fin, and if so, what shape and size to design it has to considered as well. The rationale for adding the attachment is to possibly maximize the frequency of the oscillations. The idea is that the attachment to the fin would provide some surface area
for the vortices to collide with and that the fin would be able to harness more of the energy from the vortices as they flow downstream. To determine what bluff body shape would be most efficient for vortex creation; a cylindrical body and square body are considered. On sharp-edged bluff bodies, separation is fixed at the prominent
edges, whereas on bluff bodies with a continuous surface curvature, the location of the separation depends both on the shape of the body and the state of the
boundary layer. At low Reynolds numbers, flow around a bluff body remains mostly laminar and stable, but when the Reynolds number increases, a critical value is reached, beyond which the flow becomes unstable and turbulent. This turbulence can lead to unsteady and disturbed wake motion, leading to vortex shedding. (Bearman). A hypothesis
is made based on the knowledge of vortex shedding and fluid dynamics stating that it is probable that a square body with an attachment on the fin
would produce higher oscillatory frequencies. The reasoning behind this premise is that the square body’s distinct corners would cause a more extreme separation of the streamlines of water creating more disturbances in the water and therefore more turbulence. This would create more vortices, but at a wider trajectory. The cylindrical
bluff body would conceptually do the same, but not as efficiently because of the smooth edges. This obstruction would allow considerably less disturbances to
the flow of the water, and therefore spawning fewer vortices.
Another factor other than frequency that illustrates the nature of the vortices is the amplitude of the oscillations. The presence of vortices induces periodic motion at a certain frequency and also and at a certain
amplitude. The optimum bluff body shape for the final prototype would be the one that causes an optimum combination of high frequency oscillations with high amplitudes. The amplitude of the oscillation would tell how strong the vortices are “punching” one another, which directly
affects how much energy can be extracted from the vortices. The energy-amplitude relationship here is extremely vital because the amplitude of a wave for example, is directly related to how much energy is found in the wave. A high energy wave is characterized by high frequencies and therefore one could conclude that if the fin on the
prototype oscillated at higher amplitudes, then higher energies are being utilized from the vortices interacting with the prototype. The energy transported by a
wave is directly proportional to the square of the measured amplitude (E= A^2).
The main source of energy for the prototype will be the vortices created in the fluid of course, but specifically it will be from the vortex-induced vibrations that occur. Since all fluids display some value of
viscosity, the flow around a smooth surfaced body for example, will be slowed down while in contact with the surface because of frictional and other inertial forces, forming the boundary layer. At some point however, this boundary layer can detach from the body because of excess
curvature. Here, vortices are formed changing the pressure distribution along the surface. When these vortices are not formed symmetrically, which occurs at a high Reynolds number, around the plane of the body, different lift forces develop, leading to a motion transverse to the flow of the fluid and a Karman vortex street results.
(Figure 3).
(Figure 3). Karman Vortex shedding
|