BEM-based Fluorescence Optical Tomography via Active Surfaces for Breast Cancer Diagnostic Imaging

GATECH RESEARCHERS

Francesco Fedele School of Civil & Environmental Engineering, Georgia Institute of Technology, Savannah campus,USA

Anthony Yezzi School of Electrical & Computer Engineering, Georgia Institute of Technology, Atlanta campus,USA

US COLLABORATORS

Anu Godavarty, dept. of Biomedical Engineering, Florida International University, Miami USA

Jeffrey P. Laible, dept. of Civil & Environmental Engineering, University of Vermont, Burlington USA

Ph.D. STUDENTS

Daniel Cook Georgia Tech Research Institute, Atlanta USA

PROJECT DESCRIPTION

The objective of the proposed research is the exploration of an innovative imaging algorithm for fluorescence tomography that is based upon the synergistic exploitation of two traditionally disparate analytical techniques such as BEM (Fedele et al. 2005) and geometric active surfaces (Alvino & Yezzi 2004, Whitkaer & Elangovan 2002).
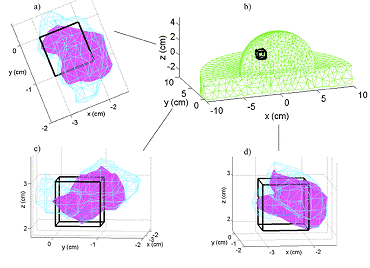
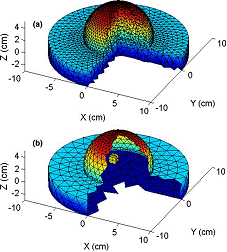
BEM is a particular numerical technique for the forward model of light propagation. It is very efficient for those applications in which the optical properties of the material to be imaged can be considered as regionally homogeneous. Using BEM, we consider the breast tissue, as a homogenous background domain volume in which is embedded a homogeneous sub-region representing the tumor tissue.  Only the surfaces of the domain and the sub-region require discretization. For example, an example BEM discretization of a breast phantom with a single cubic inclusion is shown in Figure 2(b) and compared to its FEM discretization counterpart.  Our preliminary results show that BEM predictions of a 708 node boundary element mesh are more accurate than FEM results of a 6956 node finite element mesh. Thus, using the coarser BEM mesh, light propagation is well modeled with both less computer time and memory allocation. 
The piece-wise homogeneous tissue model exploited by the BEM method is also ideally suited for a class of geometric evolution techniques known as Active Surfaces which have become one of the more promising recent computational and mathematical methods in biomedical imaging over the past two decades.  Active Surfaces in 3D (or Active Contours in 2D) are geometric representations of a potentially complicated interface between an object and its background (tumor and breast tissue in our case) which are typically evolved numerically via gradient descent flow equations designed to minimize an energy functional which depends upon both the unknown surface as well as available data measurements. These energy functionals are designed based on a model and the properties of the problem at hand and vary according to the specifics of the problem. However, a common property shared by the wide variety of Active Surface or and Active Contour energy functionals is that they are “geometric”, meaning that the evaluation of the energy for a given surface or contour does NOT depend upon how the surface/contour is represented (the choice of parameterization or of implicit embedding function is irrelevant).  Since most Active Surface or Active Contour energies are not convex, and since the geometric nature of the energies and their regularizing terms makes most direct fixed-domain representations of the unknown surface/contour (e.g. fixed parameterizations) impractical, the most common minimization method is gradient descent via a resulting geometric partial differential equation (PDE).

RELATED PEER-REVIEWED PUBLICATIONS

Fedele F. , Eppstein M. , Laible J.P.,Godavarty A. & Sevick-Muraca E.M. "Fluorescence Photon migration by the Boundary Element Method"  Journal of Computational Physics vol. 210, issue 1 pp. 109-132, 2005

Eppstein M. , Fedele F., Laible J. P., Zhang C. , Godavarty A. & Sevick-Muraca E. M. 2003 A comparison of exact and approximate adjoint sensitivities in fluorescence tomography.  IEEE Transactions on Medical Imaging, vol. 22, No. 10, pp. 1215-1222

Fedele F., Laible J. P. &  Eppstein M. 2002 Coupled complex adjoint sensitivities for frequency-domain fluorescence tomography: theory and vectorized implementation. Journal of Computational physics, Vol. 187, Issue 2, pp. 597-619

RELATED PEER-REVIEWED CONFERENCE PROCEEDINGS

Fedele F., Laible J. P. &  Eppstein M.A boundary element solution of the coupled fluorescence diffusion equations OSA Advances In Optical Imaging and Photon Migration (AOIPM) April 14-17 2004 Miami Beach FL (USA)
Laible J.P., Fedele F. &  Eppstein M. A boundary element approach to optical and fluorescence tomography.   BIOS 2003 25–31 January 2003, San Jose, California, USA  (SPIE 4955-33)  (abstract)

Fedele F., Laible J. P.,  &  Eppstein M. Fluorescence tomography using the boundary element method  SIAM Conference on Computational Science and Engineering February 10-13, 2003 San Diego CA  (abstract)

Fedele F., Laible J. P., Eppstein M.Generalized Adjoint Sensitivities of the Coupled Frequency Domain Fluorescence Diffusion Equations,  OSA Advances In Optical Imaging and Photon Migration (AOIPM) April 7-10  2002 Miami Beach FL (USA) pp. 371-373